LORA: LOW-RANK ADAPTATION OF LARGE LAN-GUAGE MODELS 学习

LoRA-overview

两种主流的高效调参策略

模型太大 Fine Tuning 调不动

adding adapter layers，就是加入额外的辅助层，LoRA 属于这种
optimizing some forms of the input layer activations，就是优化输入层，相当于优化输入的 prompt ， P-Tuning 属于这种

自己试了一下， LoRA 效果比 P-Tuning 好，但 LoRA 对显卡要求高。

数学基础

\( W_o \in \mathbb{R}^{i \times o} \) : 表示原始矩阵
\( W_f \in \mathbb{R}^{i \times o} \) : 表示 Fine-Tuning 后得到的矩阵
\( W_l \in \mathbb{R}^{i \times o} \) : 表示通过 LoRA 得到的矩阵

期望得到 \[ W_l \approx W_f \]

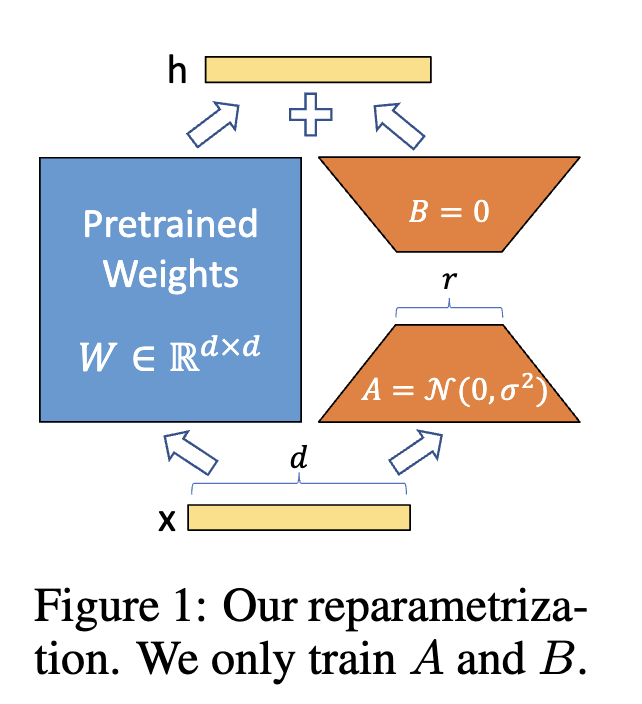
对于 \( W_l \) 可以用 \( W_o + \Delta W \) 表示，根据论文的假设

We take inspiration from Li et al. (2018a); Aghajanyan et al. (2020) which show that the learned over-parametrized models in fact reside on a low intrinsic dimension. We hypothesize that the change in weights during model adaptation also has a low “intrinsic rank”, leading to our proposedLow-Rank Adaptation (LoRA) approach.

就是说

大模型具有低秩性，实际上用低维矩阵即可覆盖整个预训练模型参数更新的信息。

这里的 \( \Delta W \) 就是那个低秩的更新矩阵。

对于低秩矩阵 \(\Delta W \) ，可以进行矩阵分解

\[ \Delta W = BA \]

其中 \( B \in \mathbb{R}^{i \times r} \) , \( A \in \mathbb{R}^{r \times o} \) r 即可以设定的参数，具体的数学原理不确定（低秩降维分解），不过反正是反向传播近似更新参数的，不过把 r 设定为矩阵 \( \Delta W \) 的秩是不是能保留最多信息？

当然论文要求 \( r \ll min(i, o) \) ，出于性能考虑。

代码实现

loralib

class Embedding(nn.Embedding, LoRALayer):
    # LoRA implemented in a dense layer
    def __init__(
        self,
        num_embeddings: int,
        embedding_dim: int,
        r: int = 0,
        lora_alpha: int = 1,
        merge_weights: bool = True,
        **kwargs
    ):
        nn.Embedding.__init__(self, num_embeddings, embedding_dim, **kwargs)
        LoRALayer.__init__(self, r=r, lora_alpha=lora_alpha, lora_dropout=0,
                           merge_weights=merge_weights)
        # Actual trainable parameters
        if r > 0:
            self.lora_A = nn.Parameter(self.weight.new_zeros((r, num_embeddings)))
            self.lora_B = nn.Parameter(self.weight.new_zeros((embedding_dim, r)))
            self.scaling = self.lora_alpha / self.r
            # Freezing the pre-trained weight matrix
            self.weight.requires_grad = False
        self.reset_parameters()

    def forward(self, x: torch.Tensor):
        if self.r > 0 and not self.merged:
            result = nn.Embedding.forward(self, x)
            if self.r > 0:
                after_A = F.embedding(
                    x, self.lora_A.T, self.padding_idx, self.max_norm,
                    self.norm_type, self.scale_grad_by_freq, self.sparse
                )
                result += (after_A @ self.lora_B.T) * self.scaling
            return result
        else:
            return nn.Embedding.forward(self, x)

这里的 lora_A 和 lora_B 就是上面说的的 BA 矩阵，在 forword 的时候就是

\[ output = Emb(x) + x A^{T} B^{T} * scaling \]

对于 Embedding 层，假设起权重矩阵为 i * o ，在加入 LoRA 后，新增了2个权重矩阵 i * r r * o ，其中 r << min(i, o) ，比如 Embedding 为 10000 * 100 的矩阵，设定 r = 8，则增加了 10000 * 8 + 8 * 100 = 80800 的参数量，相对原来增加了 80800 / (10000 * 100) = 8.08% ，也就是说使用 LoRA 后只要微调原来参数量的 8% 就行。

实验结果

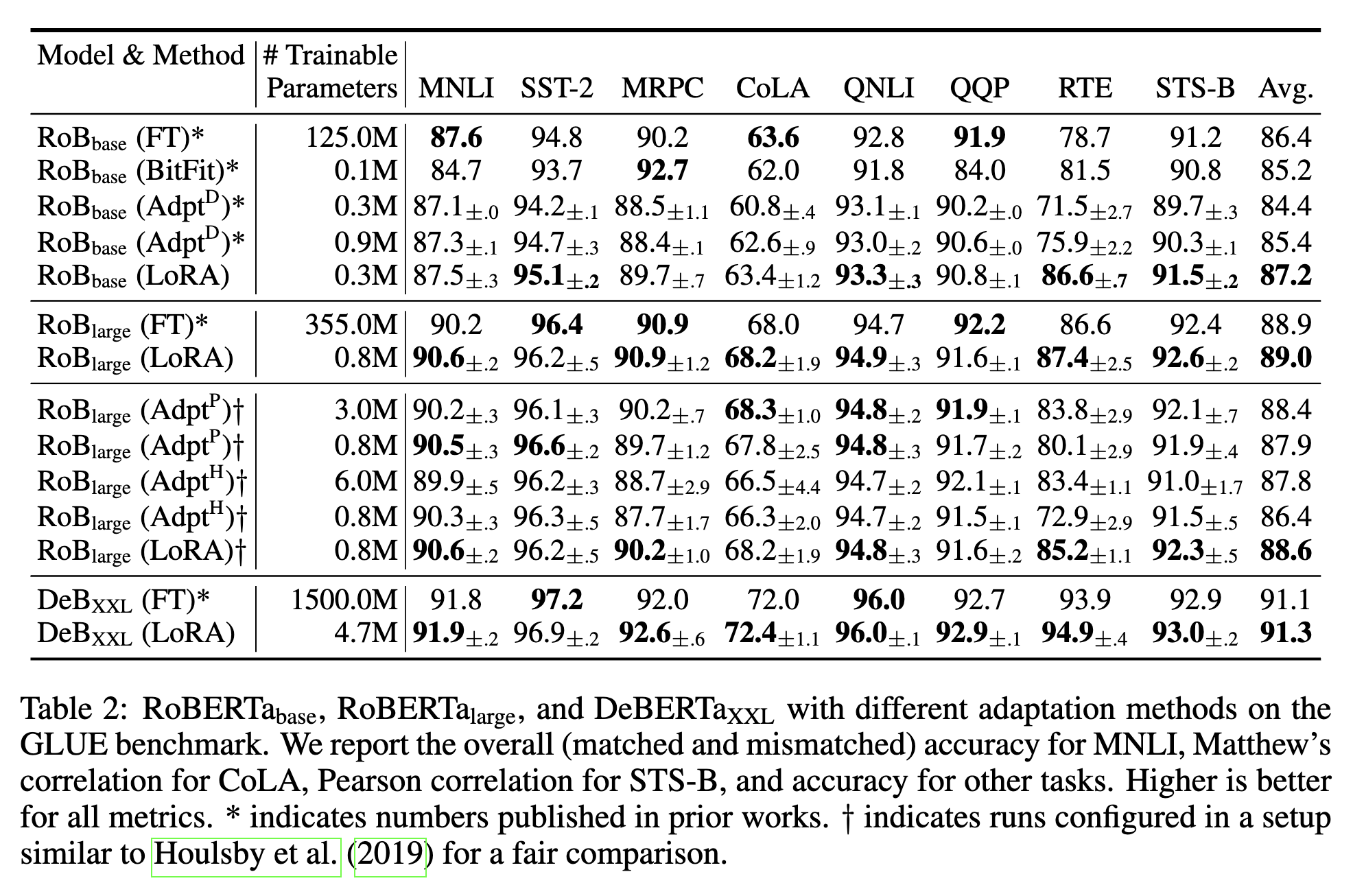
exp-data

效果非常好，比 FineTuning 都好？？训练的参数量相差百倍级别。

利用peft进行训练

peft

from transformers import AutoModelForSeq2SeqLM
from peft import get_peft_config, get_peft_model, LoraConfig, TaskType
model_name_or_path = "bigscience/mt0-large"
tokenizer_name_or_path = "bigscience/mt0-large"

peft_config = LoraConfig(
    task_type=TaskType.SEQ_2_SEQ_LM, inference_mode=False, r=8, lora_alpha=32, lora_dropout=0.1
)

model = AutoModelForSeq2SeqLM.from_pretrained(model_name_or_path)
model = get_peft_model(model, peft_config)
model.print_trainable_parameters()
# output: trainable params: 2359296 || all params: 1231940608 || trainable%: 0.19151053100118282

LLM LoRA 调参学习